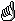Description of the procedure for deriving anatomy tables
(Brien (2017c); Brien (2019b).)
The following diagram illustrates the procedure for deriving anatomy tables, ANOVA-like tables that are useful in assessing the properties of a proposed design, irrespective of whether an analysis of variance is to be used to analyse the data. An anatomy table exhibits the confounding that occurs in every design by aligning confounded sources in different columns of the table. Two examples of the derivation of anatomy tables are available, including R scripts and output: a two-phase sensory experiment and a two-phase wheat experiment. Further examples are available in the Supplementary materials for Brien (2017c).
A description of the procedure follows the diagram or you can go to the description for a particular rectangle by clicking on it. The first two steps of the procedure, which are the same as those for formulating an allocation-based mixed model for an experiment, amount to establishing the factor-allocation description for a design.
The function designAnatomy from dae, a package for the R statistical computing environment and the GenStat procedure ACANONICAL can be used to produce the anatomy table, wiothout expected mean squares, from the intratier formulae, without the need to include pseudofactors. Then the expected mean squares can be added manually, as described below to form the .anatomy table, with expected mean squares.
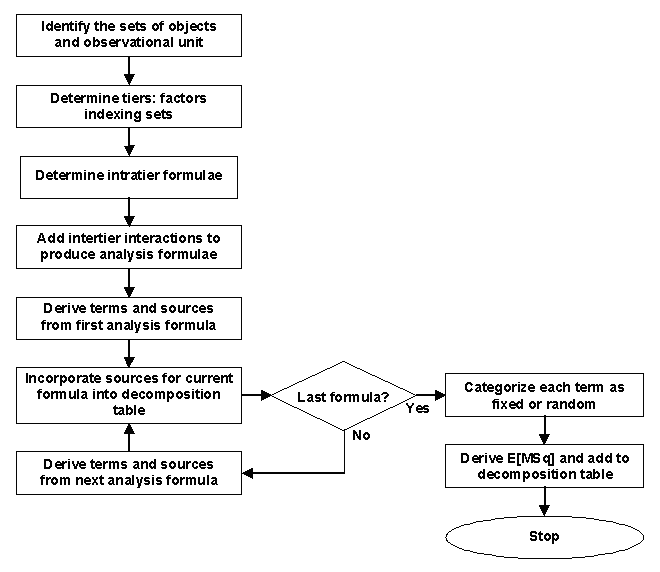
- Sets of objects and observational unit Firstly, the sets of objects involved in the allocations in the experiment are identified. Then the set of objects that are the observational units is identified. Federer (1975) defines this to be 'the smallest unit on which an observation is made'. An advantage of using the observational unit rather than the experimental unit is that for each response variable there is only one type of observational unit in an experiment whereas it is clear from Federer (1975) that there might be several different types of experimental unit. Thus, it should be easier to identify the observational unit.
- Tiers The crucial feature of the procedure is that the factors are divided into sets or tiers, as described by Brien, Harch, Correll and Bailey (2011) and Brien (2022), according to their status in the allocations that were performed in designing the experiment. Those factors that are nested within other factors and the factors that nest them also need to be identified. It can be useful to depict the allocations in a factor-allocations diagram, in which there is a panel for each tier. For multitiered experiments there will be at least three tiers. It is vital for determining the tiers that all the factors involved in the experiment are identified.
- Intratier formulae One then uses each tier, and the nesting and crossing relationships between the factors in the tier, to form an intratier formulae for the tier. It may also be necessary to include pseudofactors in some formulae and indicate that some factors are independent of others. The notation we use in the formulae is that described by Brien and Demétrio (2009, Table 1). A*B indicates that the factors A and B are crossed, A/B indicates that the factor B is nested within the factor A, A+B indicates that the factors are independent and A//B indicates that B is a pseudofactor to A. A factor-allocation diagram is useful in formulating these, the factors in a tier being those within a panel of the diagram.
- Analysis formulae These are obtained from the intratier formulae by considering for each whether crossed or nesting relationships between the factors in the current intratier formula and those in other formulae are appropriate. Often, but not always, there is a one-to-one correspondence between the intratier formulae and the tiers. There is not when some factors occur in more than one analysis formula, because factors can occur in only one tier. Also, sometimes there are less and sometimes more analysis formula than tiers.
- Anatomy table Now form the anatomy table by going around the loop shown in the above figure. The process begins with the analysis formula involving only factors whose levels are intrinsically associated with the observational units - terms involving these factors make up the initial anatomy table. This table is extended by incorporating the terms from the second analysis formula into it as described below. The extended anatomy table is further extended by incorporating the terms from each of the other analysis formulae until the terms from all analysis formulae have been incorporated into the anatomy table.
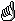
For each analysis formula in turn, a circuit of the loop to extend the anatomy table proceeds as follows:- Derive the terms and sources from the current formula Expand the analysis formula using rules such as are given in Wilkinson and Rogers (1973) or Heiberger (1989); Monod and Bailey (1992) give details on the handling of pseudofactors. If the factors A and B are crossed (A*B in a formula), these rules lead to the terms A, B and A^B being included in the analysis where A^B represents the generalized factor formed from the factors A and B. If factor B is nested within factor A (A/B in a formula), the standard rules lead to the terms A and A^B.
More generally, for formulae L and M:where gf(L) is the generalized factor formed from the tier factors in L and L^M is the sum of products of all pairs of terms in L and M.L / M = L + gf(L)^M L * M = L + M + L^M
As an example of using the rules for a more complicated formula we expand (A*B)/(C*D):
The source for each term is derived as follows:(A*B)/(C*D) = (A*B) + A^B^(C*D) = (A + B + A^B) + A^B^(C + D + C^D) = A + B + A^B + A^B^C + A^B^D + A^B^C^D - Form the generalized factor from those factors in the term that nest at least one of the other factors in the term.
- List all the factors that are not in the generalized factor of the nesting factors, each separated by ‘#’. Then add the to the end of the list the generalized factor of the nesting factors, placing it between square brackets.
A + B + A#B + C[A^B] + D[A^B] + C#D[A^B]
In this set of terms, the term C#D[A^B] stands for the interaction between C and D nested within each combination of the levels of A and B; that is [A^B] represents the combinations of A and B. - Incorporate current sources and their degrees of freedom into the anatomy table.
Add a major column to the anatomy table consisting of columns for the sources, degrees of freedom and, if the sources being added were allocated using a nonorthogonal design, efficiency factors for the current analysis formula. If the current formula is the first formula, which contains only recipient factors, the column will consist of a row for each source from that formula. When incorporating sources from other than the first formula, place them in the new major column alongside the sources already in the anatomy table with which they are confounded. This amounts to determing the experimental units for the generalized factor corresponding to a source. All sources from the same formula confounded with a particular term will be listed one under the other with the row for the term, with which they are confounded expanded to fit them. Also, if there are Residual degrees of freedom, a Residual source will need to be added, under the list of terms from the current formula. The number of Residual degrees of freedom is equal to the difference between those of the original source and the sum of the degrees of freedom of the sources incorporated under it.
Sources that arise in two consecutive formulae will not have a line entered for the formula incorporated last. When two sources are totally aliased, such as can occur with fractional factorial experiments, one will be omitted from the analysis and a note of it made separate from the anatomy table.
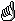
- Derive the terms and sources from the current formula Expand the analysis formula using rules such as are given in Wilkinson and Rogers (1973) or Heiberger (1989); Monod and Bailey (1992) give details on the handling of pseudofactors. If the factors A and B are crossed (A*B in a formula), these rules lead to the terms A, B and A^B being included in the analysis where A^B represents the generalized factor formed from the factors A and B. If factor B is nested within factor A (A/B in a formula), the standard rules lead to the terms A and A^B.
- Categorize terms as fixed or random
- One possible categorization of the terms is that all are classifed as random, except those terms that have only ever been allocated. This would lead to an analysis that is equivalent to a randomization analysis when all allocation is by randomization.
- Another possibility is that each factor could be categorized as fixed or random. Then a term is fixed provided that it involves only fixed factors or as random if it involve a random factor.
- Otherwise, one could independently categorize each term as fixed or random. In the end fixed terms are ones that allow for arbitraty differences between the effects whereas random terms require that the effects conform to a probability distribution, usually normal.
- Derive the expected mean squares and add them to the anatomy table
The rules for deriving the expected mean squares (EMSs) given here are based on results given by Brien (1992) and Bailey and Brien (2016). They apply to experiments in which all phases are structure balanced and may apply when they are not. For example, it can be used when all random terms are in structure-balanced tiers and, in some cases, when they are only first-order balanced. These conditions can be checked using thedesignAnatomyfunction in theRpackagedae. For all structure-balanced designs, allordersare one and there is no partial aliasing; an orthogonal design is a structure-balanced design for which allaefficiencyvalues are one. A design that is not structure balanced, but is first-order balanced, is the same as a structure-balanced design, except that it involves partial aliasing. These rules deal with experiments in which fixed sources are confounded with other fixed sources and when intertier interactions are involved.
Note that an EMS is the sum of squares of the projection of the response variable Y into the subspace for a source, divided by the dimensions of the subspace. If A is the projection matrix for a source and νA is its rank or degrees of freedom, then its EMS is (AYT(AY)/νA, which can be written as the quadratic form YT(A/νA)Y. That is, an EMS is the sum of squares of AY divided by νA, which is a quadratic form in Y, the matrix of the quadratic from being the scaled projection matrix A/νA.
Let E[Y] = ψ and Var[Y] = V. Then, the general form of an EMS [Searle (1971) Linear models. Wiley, New York. Section 2.5] is: E[YT(A/νA)Y] = trace({A/νA}V) + ψT(A/νA)ψ.
That is, an EMS is made up of two parts, a random contribution, trace(AV)/νA, and fixed contribution, ψT(A/νA)ψ. The fixed contribution is denoted by θ and is itself a quadratic form in ψ. The random contribution is a function of the canonical components, the φs.
The rules are now presented.
For each row in the anatomy table: The EMS consists of the sum of contributions for each source associated with the row, these sources being the right-most source in the row and those sources with which it is confounded; these sources come from different major columns of the anatomy table. Determine the EMS for a row as follows:- Obtain the random contribution for each contributing source in the row:
- The random contribution for a source is a linear combination of the canonical components for terms from the same major column as the source.
- Beginning with the left-most column of sources and continuing across to the right-most source for that row, obtain the linear combination that is the random contribution for each of these sources (ignore Residual sources) as follows:
- For the current source, identify the term: it is comprised of all factors in the source and is referred to as the current term. Both are represented by abbreviated names formed from the initial capital letters of the factors that comprise them. If the current source is not from the first major column and it is confounded with the sources from major columns to its left, ascertain the value of the A-efficiency criterion for the current source in the current row, the value being the harmonic mean of its canonical efficiency factors.
- For the current source, determine its random contribution to the EMS for the row:
- It is the linear combination of the canonical components for all random terms to which the current term is marginal; i.e. the current term will be a subspace of the column space for each of these random terms.
- If the current term is random, also add its canonical component to the linear combination.
- The coefficient of each canonical component in the linear combination is the number of replicates of the observed combinations of the levels of the factors in the component's random term; it is calculated as the number of observations for which the experimental design has been generated divided by the number of observed combinations of the levels of the factors in the component's random term.
- If the current source is not from the first major column, then The linear combination is now multiplied by the value of the A-efficiency criterion for the current source in the current row.
- Beginning with the left-most column of sources and continuing across to the right-most source for that row, obtain the linear combination that is the random contribution for each of these sources (ignore Residual sources) as follows:
- Form the EMS for the row:
- It is the sum of the random contributions of its sources, i.e. the sum of the linear combinations, to which is added a fixed contribution, provided at least one fixed source is involved in the row.
- The fixed contribution for a row, θ, is a quadratic form in the expectation for a response, as described above. Here, the θ for a row is specified by nominating the matrix of the quadratic form for the row using a subscript that is a list of the abbreviated names for sources in the row, beginning with the left-most source and proceeding to the right-most source and with sources separated by left arrows (←). The left arrow indicates that the source at the tail is confounded with the source at the head of the arrow; thus, the matrix of the quadratic form is the scaled projection matrix for the part of the source at the head that pertains to the source at the tail. All sources are fixed unless they are asterisked, in which case they are random sources; note that while the projection matrix may incorporate random sources, only fixed sources have terms that contribute to the expectation.
- Suppose that we have allocated source A confounded with recipient source B. Thus, θB*←A
indicates that the matrix of the quadratic form is the sclaed projection matrix for the part of B that pertains to A, where A is fixed and B is random. Consider the θs for the four combinations of the A and B sources being either fixed or random:
- Both fixed:
- θB←A;
- Only A fixed:
- θB*←A or, if A is only confounded with B, θA; while B may be incorporated into the projection matrix for the quadratic form, it is not involved in the expectation;
- Only B fixed:
- θB←A* and θB⊢, where B⊢ means that part of the recipient source B that is orthogonal to all allocated sources; A only plays a role in the projection matrix for the quadratic form, it making no contribution to the expectation;
- Both random:
- no θ is applicable.
- If there is no allocated source confounded with B and B is fixed then the θ is θB.
The resulting table is an anatomy table, with expected mean squares.