Factor-allocation description/diagrams

Factor-allocation description

A fundamental aspect of the approach used to describe experimental designs, and so to develop models for the analysis of the resulting data arising from them, is that it is based on the factor-allocation description for the design. The factor-allocation description for a design is displayed in its factor-allocation diagram. The first two steps of deriving the anatomy table for a design and for formulating an allocation-based mixed model for an experiment will have been accomplished once the factor-allocation diagram for the design has been produced. Brien, Harch, Correll and Bailey (2011) and Brien (2017c) describe this approach and compare it to single-set description.

Factor-allocation description is so-named because it is a description of an experimental design that encapsulates the allocation employed in the design. Crucial to doing this is the division of the factors associated with the experimental design into sets on the basis of the role that they play in the allocation. For a single allocation, the factors are divided into those that are allocated and those which are recipients of the allocated factors. When there are multiple allocations in an experimental design, then there is an allocated and a recipient set of factors for each allocation, with some sets being allocated in one allocation and recipient in another.

Factor-allocation diagrams

Factor-allocation diagrams, introduced by Brien, Harch, Correll and Bailey (2011), are an extension of the randomization diagrams that Brien and Bailey (2006) developed. Their purpose is to display, not only the randomized, but also the nonrandomized allocations of factors in an experiment. They describe the allocation of multiple sets of objects, showing in a panel for each set of objects their associated tier of factors and the nesting and crossing relations among the factors within the tier. For example, the following factor-allocation diagrams is Figure 25 for the nonorthogonal two-phase sensory experiment from Brien and Bailey (2006), which, because all allocations in the experiment are randomizations, is a randomization diagram.

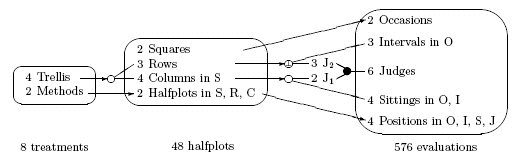
Randomization diagram for two-phase sensory experiment

The conventions used in such a diagram are as follows:

Each panel in the diagram lists the factors in a tier, along with their numbers of levels and nesting relations. A factor that is nested is followed by `in' and a list of the first letters of the names of the factors within which it is nested.
Pseudofactors are sometimes needed to aid an allocation and these are added between panels. A pseudofactor is named using the initial letter of the factor and a numeric subscript. Hence, J₁ is a two-level pseudofactor for Judges.
An arrow from left to right indicates that the factor(s) to the left are being randomized to the factors(s) to the right. Thus, Methods is randomized to Halfplots. If the arrow is dashed, it indicates that the asignment was systematic, rather than random (see Figure 27 in Brien and Bailey, 2006).
A ‘●’ with two or more lines leading to it from the left (or away from it on the right) signifies the observed combinations of the levels of the factors on the left (or on the right) from the same panel/tier. A ‘■’ is used if the factors are from different tiers.
The purposeful selection of a fraction of the combinations of some factors is indicated by dashed lines to a circle to which an ‘f’ is added to either ‘○’ or a ‘□’; then an arrow leads from the circle or square to indicate the factors to which the fraction is randomized or a dashed arrow used if the assignment is systematic.
When randomization is to the combinations of the levels of two or more factors, four possibilities are distinguished:
1. They are completely randomized, in which case either a ‘●’ or a ‘■’ is used at the source of the lines going to the factors depending on whether the factors are from the same panel/tier This possibility is unlikely to occur in practice because it implies that one is completely randomizing to the combinations of two factors whose separate effects are of interest. For example, it is unlikely that Treatments would be completely randomized to the unit factors Rows and Columns when these are considered to be crossed..
2. A nonorthogonal design is used, in which case either ‘○’ or a ‘□’ is used depending on whether the factors are from the same panel/tier. For example, Trellis is randomized the combinations of Rows and Columns using Youden squares that are balanced but nonorthogonal.
3. An orthogonal design is used, in which case a ‘⊥’ is added to either ‘○’ or a ‘□’. For example, Rows are randomized to the combinations of Intervals and J₂ using Latin squares.
4. A spatial design is used, in which case a ‘ρ’ is added to either ‘○’ or a ‘□’; also, a dotted arrow to the circle is used to indicate that the assignment is not randomized in the sense of Brien and Bailey (2006).
A ‘◆’ indicates that the factor(s) or pseudofactor(s) to the left directly determine pseudofactors of factors to the right (see Figure 16 in Brien and Bailey, 2006).
A ‘◇’ indicates that a nonorthogonal design, between the factor(s) or pseudofactor(s) to the left and the factors to the right, is used to determine pseudofactors of factors to the right. A ‘⊥’ is added to the ‘◇’ if an orthogonal design is used.
A dashed oval surrounds the panels making up a pseudotier, indicating that the factors in those panels are combined to form the pseudotier. All factors in the pseudotier are then directly involved in a randomization, they being either randomized to a tier (see Figure 16 in Brien and Bailey, 2006) or having a tier randomized to them (see Figure 18 in Brien and Bailey, 2006).

Factor-allocation versus Single-set description

As Brien, Harch, Correll and Bailey, (2011) suggest, experiments are also commonly described using what can be termed single-set description. In this approach one identifies the smallest set of factors, including the factors of interest to the researcher, that is sufficient to uniquely index the units in the experiment. This may necessitate the incorporation of a single synthetic factor that is nested within the other factors and whose levels differ for the repeats of the combinations of the other factors. Generally, the factors identified in this approach are a subset of those from the factor-allocation approach, the subset being sufficient to uniquely index the units. Usually unit factors that are `equivalent' to treatment factors are omitted, this being feasible because it is impossible to observe all combinations of these factors.

Consider the first-phase of the two-phase sensory experiment, for which the design was a factorial randomized comnplete-block design with the factors Rosemary and Irradiation randomized to Meatloaves within Blocks. The single set approach would identify the factors for this experiment as being Blocks, Rosemary and Irradiation and these factors uniquely index the observational units. That is, the factor Meatloaves is omitted in the single-set description. The following tables compare the anatomy table from the factor-allocation description with that from the single-set description.

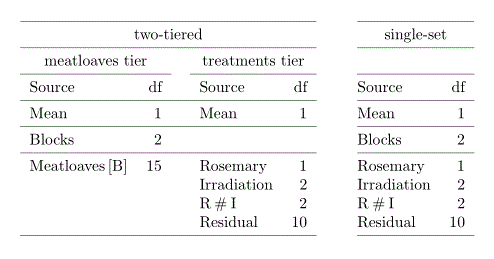
Problems with the single-set description

While the factor-allocation and single-set description do lead to the same analysis, the use of the single-set description has the following limitations as compared to the factor-allocation description.

Does not display confounding: With a single-set based analysis each contrast is associated with only a single term and so there is no indication of the multiple sources associated with some of the contrasts as a result of the confounding arising from the allocation. For example in the two-tiered anatomy table derived from two structure formula it is clear that the one degree of freedom associated with Rosemary is confounded with Meatloaves[Blocks]. With the single-set analysis there is only the term Rosemary associated with this one degree of freedom. Crucial to achieving the exhibition of the confounding in an experiment is to include all of the factors to which factors have been allocated and to divide the factors into sets for determining the confounding relationships between sources based on the factors fron different sets. In the example, the inclusion of the Meatloaves factor to which Rosemary and Irradiation have been allocated is the key, it having been omitted in the single-set description. Then the confounding of Rosemary, Irradiation and R#I with each of Mean, Blocks and Meatloaves[B] can be investigated.
Does not correctly identify sources of variation: It is very important to understand that we do not regard the Block interactions with Rosemary and Irradiation as indicating actual sources of variation for which we are including terms in the model. Rather they are merely convenient way of obtaining the sums if squares. Summing these interactions is one way of obtaining the Residual for Meatloaves[Blocks]. However, the term in the model is Meatloaves[Blocks], not Blocks#Rosemary + Blocks#Irradiation + Blocks#Rosemary#Irradiation. So we have a term for variability between meatloaves within a block in the model and we are assuming that there is no interaction between blocks and rosemary and irradiation treatments.

For further information see Brien, Harch, Correll and Bailey, (2011, Section 3.2).